English version with more details and references: Lazzarini’s little sticks
Het stokje van Lazzarini
De Italiaan Mario Lazzarini zei in 1901 dat hij de waarde van pi met een apparaatje tot op zes decimalen nauwkeurig had benaderd. Wiskundigen kunnen zich er nog altijd over opwinden.
door Hans van Maanen – Skepter 31.3 (2018)
EEN ‘gruweldaad’ noemde de hoofdredacteur van Nature het. ‘Laat het een waarschuwing zijn aan allen die de literatuur vervuilen, dat hun wandaden ze tot in het graf zullen volgen.’
Aanleiding voor de toorn van John Maddox, uitgestort in augustus 1994, was een vier maanden eerder verschenen artikel van de Amerikaanse wiskundige Lee Badger. Die had zich op zijn beurt verdiept in een ruim negentig jaar eerder verschenen artikel van een Italiaanse collega, en wiskundig vastgesteld dat het resultaat onmogelijk kon kloppen — er moest ofwel sprake zijn van onvoorstelbaar geluk, ofwel van bedrog. Die collega was Mario Lazzarini, en zijn artikel, uit 1901, ging over een experimentele bepaling van het getal pi — het getal dat wij het best kennen uit de wiskundige formules voor omtrek en oppervlak van de cirkel. Maddox wond zich werkelijk erg op: ‘De waarheid is, dat als Lazzarini’s resultaat in 1994 was gepubliceerd en niet in 1901, het schaamteloze oplichterij zou worden genoemd.’ Mijn vermoeden is, dat als Maddox het artikel van Lazzarini had gelezen en niet dat van Badger, hij een rood hoofd van pret en niet van woede zou hebben gekregen.

Parketvloer
Het idee om pi niet met behulp van de wiskunde, maar met behulp van een experiment te benaderen, heeft een lange geschiedenis. De achttiende eeuw was de eeuw waarin wiskundigen de kansrekening — het uitrekenen van weddenschappen — ontdekten. Die leverde talloze oplossingen voor problemen die daarvoor onkraakbaar leken, en uiteraard ook talloze nieuw te kraken problemen. Een ervan werd in 1777 gesteld door de Franse geleerde George-Louis Leclerc, graaf van Buffon. Hij opperde in zijn Essai d’arithmétique morale:
Ik stel me voor dat in een kamer, waarvan de parketvloer eenvoudig uit evenwijdige planken bestaat, een stokje wordt opgegooid, en dat een van de spelers wedt dat het stokje geen naad van het parket raakt, de ander daarentegen dat het stokje wel een van de naden raakt; gevraagd wordt het lot van deze twee spelers.
Hij voegde er, cursief en wel, aan toe dat ‘men dit spel kan spelen op een dambord met een naainaald of een koploze speld.’
Met wat simpele hogere wiskunde toonde hij aan dat de kansen voor de twee spelers gelijk zijn als de lengte van het stokje ongeveer drie vierde is van de breedte van de planken. Vervolgens berekende hij ook nog hoe het zat met het lot van de spelers als een stokje op een vloer met vierkante tegels terechtkomt en als een munt op een tegelvloer komt.
Bijna vijftig jaar later, in 1812, pakte zijn landgenoot Pierre-Simon markies van Laplace de draad op en hij kon, in zijn Théorie analytique des probabilités, uitrekenen wat de absolute kans is dat ‘een zeer dunne cilinder’ een lijn raakt. (*) Die hangt uiteraard af van zowel de lengte van de cilinder als de afstand tussen de lijnen. Laplace noemde de lengte van het stokje 2r en de afstand a (en ‘pi’ noteerden wiskundigen toen sinds kort met de Griekse letter π):
Als men deze cilinder een groot aantal malen opwerpt, zal de verhouding tussen het aantal keren dat de cilinder een lijn raakt en het totaal aantal worpen vrijwel gelijk zijn aan de waarde 4r / π, hetgeen de waarde van de omtrek van de munt 2π oplevert.
 Naald van Buffon
Naald van Buffon
En dat levert niet alleen de oplossing van het probleem, maar ook een aardige manier om pi proefondervindelijk te bepalen: als we de lengte van het stokje en de afstand tussen de lijnen weten, rolt pi er, na heel veel keren gooien, vanzelf uit. Het kan ook met een naald of een koploze speld, en dat experiment is, hoewel Buffon het dus in het geheel niet heeft voorgesteld, bekend geworden als de ‘naald van Buffon’: gooi een naald op een gelinieerd oppervlak, houd het aantal treffers T en het totaal aantal worpen N bij, en bereken pi volgens de aanwijzingen van Laplace (nu is l de lengte van de naald, a is weer de afstand tussen de lijnen):
pi = (2l / a) × (N / T)
Dus als bijvoorbeeld de naald 25 millimeter lang is en de afstand tussen de lijnen 26 millimeter, krijgen we na 100 keer gooien en 60 treffers een schatting van pi van 3,205 128 (zoveel cijfers achter de komma is natuurlijk onzin, daarover later meer).
Proef op de som
Er zijn werkelijk mensen geweest die geprobeerd hebben op deze manier pi te benaderen. Als ze van tevoren hadden uitgerekend hoeveel pogingen ze moeten doen om zelfs de eerste decimaal met redelijke zekerheid te kunnen bepalen, zouden ze het wel uit hun hoofd hebben gelaten, maar de vasthoudendheid van wiskundigen moet men nooit onderschatten.
We zullen de helden niet allemaal noemen – uit de populairwetenschappelijke boeken halen we M. A. Smith in 1855 met 3204 worpen en een pi van 3,1553, August de Morgan met 600 worpen en 3,137, en een Amerikaanse kapitein Fox die na 590 worpen op 3,1416 uitkwam. Die laatste poging is zeker fraai, gezien de ware waarde:
π = 3,141 592 653 589 793 238 462 …
Maar het goud voor de nauwkeurigste benadering ooit ging dus, in 1901, naar de hierboven genoemde Mario Lazzarini. Hij rapporteerde, met 3408 worpen en 1808 treffers, een verbluffend mooie benadering: 3,141 592 9 — correct tot op de zesde decimaal. Dat was de gruweldaad waarin John Maddox 93 jaar later bijna stikte.
Het klinkt ook, op het eerste gehoor, veel te mooi om waar te zijn, en uiteraard werd al aan de betrouwbaarheid van Mario Lazzarini getwijfeld voordat Lee Badger en John Maddox zich ermee bemoeiden. Hoewel — het is eerder opmerkelijk dat zoveel wiskundigen zijn bevindingen serieus namen en er werkelijk een mooie illustratie van wiskundig en experimenteel vernuft in zagen. Ook hier zullen we niet iedereen noemen, maar we vinden in de literatuur namen als George Gamow, Jacob Bronowski en Edward Kasner en James Newman — ‘Een mooier voorbeeld van de verbondenheid van alle takken van de wiskunde is amper denkbaar,’ schrijven de twee laatsten enthousiast in hun Mathematics and the imagination uit 1940.
‘Onwelriekend’
De eerste die de fraaie resultaten van Lazzarini als ‘onwelriekend’ verdacht maakte, was de Canadese wiskundige Norman Gridgeman, in een artikel in het tijdschrift Scripta Mathematica (dl. 25 (1960), p. 183–195). Een jaar later, op 8 juni 1961, wijdde Thomas O’Beirne zijn rubriek ‘Puzzles and paradoxes’ in New Scientist aan de kwestie — overigens zonder het artikel van Gridgeman te kennen.
Allengs werden de poten verder onder Lazzarini weggezaagd, tot Lee Badger met zwaar wiskundig geschut de genadeklap gaf, in Mathematics Magazine van april 1994 (dl. 67, p. 83–91). Allemaal spraken ze er in meer of minder bedekte termen schande van en twijfelden ze aan de integriteit van de Italiaan.
Wiskundeleraren
Mario Lazzarini publiceerde zijn artikel in de Periodico di matematica per l’insegnamento secondario (jg. 17 (1901), p. 140–143). Dat is, zoals uit de naam blijkt, geen wiskundetijdschrift, maar een tijdschrift voor wiskundeleraren. Dat maakt uit voor het vervolg; in alle artikelen over Lazzarini wordt het blad steevast Periodico di matematica genoemd alsof het een gezaghebbend wetenschappelijk tijdschrift betrof.
En of Lazzarini werkelijk een ‘Italiaans wiskundige’ was, zoals hij altijd wordt voorgesteld, staat daarmee ook op losse schroeven: het ligt meer voor de hand dat hij wiskundeleraar was — blijkens de ondertekening van een ander artikel van zijn hand in de Periodico waarschijnlijk in Massa in Toscane.
Een zoektocht naar zijn verdere antecedenten, voor mij ondernomen door de Italiaanse bibliothecaris Ilaria Vercillo, leverde geen nadere gegevens op. Hij lijkt niets wetenschappelijks te hebben gepubliceerd buiten een paar artikelen in de Periodico en een hoofdstuk in een boek over Fibonacci; hij is in de mist van de geschiedenis van de wiskunde opgelost.
Wasmachine
In diezelfde mist is echter ook de gehele proefopstelling van Lazzarini verdwenen — en dat is jammer, want dat biedt zijn critici des te meer gelegenheid hem in een kwaad daglicht te stellen. Gridgeman had zijn mening al klaar voordat hij het artikel van Lazzarini had gelezen en vertelt maar de helft van het verhaal, O’Beirne en Badger nemen al evenmin de moeite uit te leggen hoe Lazzarini’s experimenten — en resultaten — precies in elkaar staken.
Terwijl Lazzarini het in zijn artikel zo omstandig uitlegt. Hij had, zegt hij, een apparaat gebouwd dat het vallen en meten geheel had geautomatiseerd.
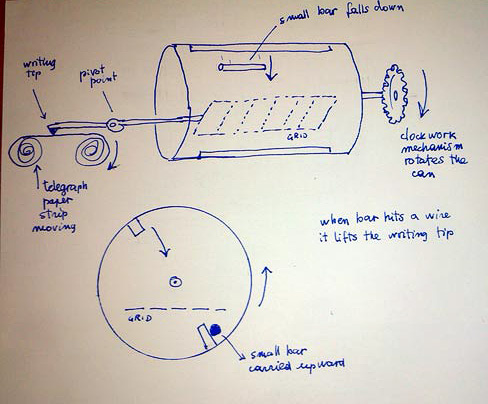
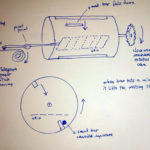
In een horizontaal draaiende cilinder zitten twee drempels overdwars (ongeveer zoals in een moderne wasmachine). Een stokje dat wordt losgelaten in die trommel, wordt door de drempel meegenomen omhoog, en valt op het hoogste punt naar beneden. Midden in de trommel zit een rooster met evenwijdig gespannen draden die door het stokje, indachtig Buffon, al dan niet worden geraakt. Als het stokje op een draad terechtkomt, gaat het rooster iets omlaag, en omdat het op een lange beweegbare as is gemonteerd, wipt het andere uiteinde omhoog. Aan dat andere uiteinde zit een schrijfstift die op een voortrollende strook telegraafpapier drukt. Gaat het rooster omlaag, dan gaat de stift omhoog en wordt de lijn onderbroken. Het stokje van Lazzarini is 2,5 centimeter, de trommel draait twaalf keer per minuut. Het enige wat de experimentator nog hoeft te doen, is het aantal onderbrekingen in de streeplijn op het papier te tellen, de waarden in de formule in te vullen, en pi komt eruitgerold. (Vertaling van de uitleg van Lazzarini.)
En hier de resultaten die Lazzarini met deze methode verkreeg — ‘Ed ecco i risultati da me ottenuti con questo mezzo.’ Eerst, zegt hij, had hij de draden op het rooster evenwijdig aan de as van de cilinder geplaatst. Dat werkte niet heel goed: de afstand tussen de draden was 2,6 centimeter, en met 100 pogingen zat hij op 60 treffers, met 500 pogingen op 276. Dat levert schattingen voor pi op van 3,205 en 3,484 (Lazzarini geeft 3,483: het lijkt erop dat hij voor het gemak steeds afkapt in plaats van afrondt).
| N | T | pi |
| 100 | 60 | 3,205 |
| 500 | 276 | 3,483 |
Dus draaide hij de bespanning een kwartslag, en nu ging het beter. Lazzarini meldt, in twee tabelletjes, twee series metingen: eerst weer met een afstand tussen de draden van 2,6 centimeter:
| N | T | pi |
| 100 | 62 | 3,101 |
| 200 | 122 | 3,152 |
| 1000 | 611 | 3,147 |
| 2000 | 1229 | 3,126 |
| 3000 | 1840 | 3,135 |
| 4000 | 2448 | 3,142 |
En dan het resultaat van de tweede serie, waarbij hij de tussenruimtes heeft vergroot tot 3 centimeter:
| N | T | pi |
| 100 | 53 | 3,144 |
| 200 | 107 | 3,115 |
| 1000 | 524 | 3,180 |
| 2000 | 1060 | 3,1446 |
| 3000 | 1591 | 3,142 |
| 3408 | 1808 | 3,1415929 |
| 4000 | 2122 | 3,1416 |
Inderdaad springt de score bij 3408 worpen eruit. Niet alleen omdat 3408 geen rond getal is, maar ook omdat pi hier opeens tot op zeven decimalen is berekend, de andere slechts tot drie of vier. En de eerste zes van die zeven decimalen zijn, zoals gezegd, correct.

Zu Chongzhi
Het is toch ondenkbaar dat ook maar iemand van Lazzarini’s collega’s dit resultaat serieus heeft genomen? Alles, maar dan ook alles, wijst in de richting van een grapje, prima bruikbaar in de wiskundelessen. Zeker als de leerlingen net de wonderbaarlijke benadering van pi hebben geleerd die de Chinese wiskundige Zu Chongzhi, 355 / 113, al in de vijfde eeuw had gevonden. Want zo zit de breuk van Lazzarini natuurlijk in elkaar:
(3408 / 1808) × (5 / 3) = 355 / 113
en in 5 / 3 herkennen we 2l / a, tweemaal de lengte van het stokje van Lazzarini gedeeld door de ruimte tussen de draden in serie II.
Even duidelijk zal het, ook voor wiskundeleraren aan het begin van de vorige eeuw, zijn geweest dat die nauwkeurigheid nergens op slaat: als teller en noemer vier cijfers hebben, mag de tiendelige breuk niet met zeven cijfers achter de komma. En dan hebben ze nog niet gewezen op de mogelijkheid van telfouten en andere haperingen. Hun leerlingen zullen meteen opmerken dat het stokje niet van het hoogste punt zal vallen, maar al na een kwart omwenteling krachteloos van het drempeltje rolt zonder ooit het rooster te raken. En dat de hele proef een beetje zonde van de moeite zou zijn: volgens Lazzarini deed zijn apparaat 24 metingen per minuut, dus dan heeft hij het, voor 8500 metingen, amper zes uur laten draaien. ’t Is een en al gekkigheid.
Maar doordat alle latere commentatoren de details van Lazzarini’s experiment en de doelgroep van het tijdschrift weglaten, lijkt het alsof onze Italiaan een grove wetenschappelijke overtreding heeft begaan. De meeste kritische auteurs noemen alleen de geïsoleerde breuk 3408 / 1808 en trekken dan meteen een rode kaart. Ook Gridgeman en O’Beirne laten de context goeddeels weg. Badger geeft de tussenresultaten van Lazzarini wel, maar vindt daarin des te meer bewijs dat er sprake is van oplichting: ook die resultaten zijn te mooi om waar te zijn, en tezamen zijn ze helemaal ondenkbaar: ‘Met de normale benadering van de binomiale verdeling is de waarschijnlijkheid kleiner dan 0,00003’. Hier wordt met een kanon op een mug geschoten.
Vrolijke wetenschap
Natuurlijk, het is niet te bewijzen dat Lazzarini de boel ter lering en vermaak in de maling nam, maar die verklaring lijkt toch een stuk aannemelijker dan die van kwade opzet. In de jaren tachtig van de vorige eeuw begon het tot wetenschappers door te dringen dat er ook in hun heiligdom gefraudeerd kon worden. Het boek van William Broad en Nicholas Wade, Betrayers of the truth, kwam in 1982 uit, en John Maddox had in 1988 de broddelwetenschap van Jacques Benveniste om de oren gekregen (zie Skepter 1991;2). Misschien was iedereen er daarom nogal scherp op.
Tegenwoordig wordt het net rond schaamteloze bedriegers allengs strakker aangetrokken, en zijn we misschien weer wat meer vertrouwd geraakt met het idee van de wetenschappelijke grappenmakerij. Dankzij de kerstnummers van het artsenblad BMJ weten we dat bidden kan helpen bij bloedvergiftiging en dat de ‘mannengriep‘ echt bestaat, maar ook andere bladen, zelfs de allergewichtigste New England Journal of Medicine, willen hun lezers nog wel eens met een grappig bedoeld artikel op het verkeerde been zetten.
Of al die vrolijke wetenschap niet alleen maar tot meer verwarring leidt, is een andere vraag – waarover Mario Lazzarini waarschijnlijk graag zou hebben meegepraat.
Literatuur
Lazzarini, M. Un’applicazione del calcolo dell probilità – alla ricerca sperimentale di un valore approsimato di π. Periodico di matematica per l’insegnamento secondario jg. 17 (1901), p. 140–143. (artikel – hele journal via webarchive)
Badger, L. Lazzarini’s Lucky Approximation of π. Mathematics Magazine Vol. 67, No. 2 (april, 1994), pp. 83-91.
Gridgeman, N. Geometric probablity an the number π. Scripta Mathematica dl. 25 (1960), p. 183–195.
O’Beirne, T. Puzzles and Pardoxes – 23: how to π with statistics. New Scientist nr. 238 (8 juni 1961), p. 598.
Maddox, J. False Calculation of pi by Experiment. Nature 370 (4 augustus 1994) p. 323. (kopie)
(*) De tekst van Laplace was in het oorspronkelijke Skepter-artikel niet correct weergegeven en is hier aangepast met dank aan Albert Otten.