De machine van Lazzarini
De Italiaan Mario Lazzarini vond in 1901 op experimentele wijze (de ‘naald van Buffon’) een opmerkelijk nauwkeurige benadering van π. Zijn werk werd decennia later als uiterst verdacht beschouwd, en door sommigen zelfs als fraude betiteld. Die beschuldiging is nogal overtrokken, betoogt Hans van Maanen in het artikel ‘Het stokje van Lazzarini’ in Skepter 31.3 (2018).
Lazzarini beschrijft in zijn artikel dat hij een apparaat bouwde dat het experiment geheel automatisch kon uitvoeren. Hieronder de vertaling van de beschrijving die Lazzarini gaf en de reconstructie die op grond daarvan te maken is.
Beschrijving van het apparaat in het artikel van Lazzarini, vertaald vanuit het Italiaans
Het apparaat dat ik heb ontworpen en voor de hieronder beschreven experimenten heb gebruikt, bestaat uit drie onderdelen.
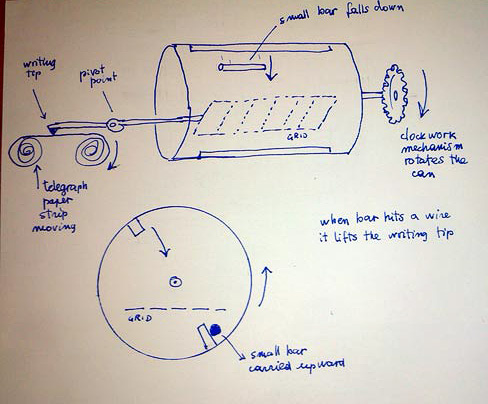
1. Een cilinder van dun metaal, 16 cm in doorsnee en 17 cm in hoogte, aan de ene zijde open en aan de andere zijde bevestigd aan een as die met een uurwerkmechaniek ronddraait. In de cilinder plaatste ik het staafje, dat dankzij twee diametraal tegenover elkaar geplaatste drempeltjes omhoog wordt getild en naar beneden valt. Daar stuit het tegen het andere drempeltje en wordt het weer omhooggetild tot het valt, waardoor we dus een ononderbroken serie krijgen zolang de cilinder draait. In mijn geval draaide de cilinder 12 maal per minuut, zodat het staafje 24 maal per minuut viel.
2. Het tweede deel van het apparaat dat ik heb gebruikt, wordt gevormd door wat ik het net zal noemen. Het bestaat uit een rechthoekig raamwerk van 8 cm bij 15 cm, waarvan de weerszijden zijn verbonden door een aantal zeer dunne, strak gespannen en evenwijdige draden. Dit net ligt horizontaal in de hierboven beschreven cilinder, en doet zo dienst als de horizontale lijnen op papier van anderen die zich voor mij de kwestie hebben beziggehouden.
3. Nu rest slechts het automatisch registreren van het aantal treffers. Daartoe is het raam bevestigd aan een horizontale as, die aan het andere uiteinde voorzien is van een schrijfstift. Een veertje drukt de stift op een strook telegraafpapier die er onderdoorloopt via hetzelfde uurwerkmechaniek dat de cilinder laat draaien. De stift schrijft dus een ononderbroken streep op het papier. Stel nu dat het vallende staafje een van de draden van het netwerk raakt, dat zoals gezegd zeer makkelijk om zijn horizontale as draait, dan gaat het iets omlaag, terwijl aan de andere kant de stift even van het papier wordt gelicht en de streep wordt onderbroken. Het veertje drukt de stift echter onmiddellijk weer terug, en op deze manier wordt elke treffer zichtbaar als een onderbreking van de streep.
Zo kunnen we, als het uurwerk eenmaal in beweging is gezet, het apparaat aan zichzelf overlaten zonder dat we erbij moeten blijven, en aan het eind van het experiment hoeven we slechts de onderbrekingen te tellen en de gevonden waarden in de formule in te vullen…
En hier zijn de resultaten die ik op deze wijze heb verkregen. Aanvankelijk had ik de korte zijden van het raamwerk met elkaar verboden, waardoor het stelsel van evenwijdige draden evenwijdig aan de drempels was. In deze opstelling was de benadering erg slecht, zoals uit de hierbij gevoegde tabel blijkt.
Een betere benadering verkreeg ik door het netwerk andersom te spannen, dus door ze aan de lange zijden van de rechthoek vast te maken. Hier zijn de experimenten in tweeën gedeeld, omdat ik, terwijl ik de lengte van het staafje gelijk hield, wel de afstand tussen de draden varieerde, en hier zijn de verkregen resultaten.
Samengevat vinden we dat de waarden […] van pi zijn: dat wil zeggen, bij 3408 keer vallen, [nauwkeurig tot de zesde decimaal].
Bron
Lazzarini, M. Un’applicazione del calcolo dell probilità – alla ricerca sperimentale di un valore approsimato di π. Periodico di matematica per l’insegnamento secondario jg. 17 (1901), p. 140–143. (artikel – hele journal via webarchive)

