Beïnvloeding van het toeval
Parapsychologische PK-experimenten
door Rob Nanninga – Skepter 22.2 (2009)
J. B. Rhine (1895–1980), de grondlegger van de experimentele parapsychologie, werd in de jaren 1930 bekend door ESP-experimenten (extrasensory perception) waarbij hij zijn proefpersonen zenerkaarten liet raden. Vanaf 1934 voerde hij ook proeven uit met dobbelstenen. Hij kwam op dit idee toen een dobbelaar hem vertelde dat veel beroepsgokkers geloven dat ze de uitkomst van een worp mentaal kunnen beïnvloeden. Rhine publiceerde de resultaten van zijn eerste experimenten met psychokinese (PK) pas negen jaar later, misschien omdat hij aanvankelijk bang was dat ze zijn geloofwaardigheid zouden ondermijnen.
Waarom denkt een proefpersoon tijdens een ESP-experiment dat er een cirkel op de te raden kaart staat en geen ster? Dat weten we niet. We kunnen niet nagaan waar zulke gedachten vandaan komen. Ze lijken spontaan te ontstaan. Veel mensen vinden het niet zo moeilijk om zich voor te stellen dat spontane gedachten kunnen worden opgewekt door factoren die wetenschappers nog niet kennen en misschien nooit zullen kunnen meten.
Het is lastiger om je voor te stellen hoe de bewegingen van materiële objecten door onzichtbare gedachtekracht zouden kunnen worden beïnvloed, zoals bij psychokinese schijnt te gebeuren. Als er sprake is van een waarneembaar materieel effect, dan zou het ook mogelijk moeten zijn om met technische apparatuur te meten welke (elektromagnetische?) kracht daarvoor verantwoordelijk is, maar dat heeft nooit wat opgeleverd. Hoewel verrassend veel professionele parapsychologen nog geloven dat het mogelijk is om voorwerpen met mentale kracht te verplaatsen, erkennen ze gewoonlijk dat het bewijsmateriaal te mager is voor de wetenschappelijke wereld. Wie er anders over denkt, heeft meestal te weinig verstand van trucs en misleiding. De sterkste staaltjes worden altijd vertoond onder omstandigheden die normale verklaringen niet uitsluiten. Als je bijvoorbeeld ziet hoe iemand op afstand een klein voorwerp verplaatst, dan moet je er wel zeker van kunnen zijn dat er geen onzichtbare goochelaarsdraad wordt gebruikt.
Bij echte parapsychologische experimenten zie je geen wonderen meer gebeuren. De dobbelsteen gaat niet vanzelf rollen en als een worp zes ogen oplevert, is dat niet echt bijzonder. Pas wanneer je alle worpen gaat tellen, kun je tot de conclusie komen dat er meer zessen zijn gegooid dan je statistisch gezien mag verwachten. Er zitten dan naar het schijnt zessen tussen die niet louter aan het toeval te danken waren, al weet je niet welke. Je hebt de dobbelsteen geen rare sprongen zien maken. Het is niet duidelijk hoe en op welk moment de beïnvloeding heeft plaatsgevonden.
Als je 6000 keer met een zuivere dobbelsteen gooit, dan mag je ongeveer 1000 zessen verwachten. Stel dat je psychokinetische kracht (wat dat ook moge zijn) bij een op de honderd worpen werkt. Dan scoor je 60 extra treffers. Dat is al meer dan voldoende voor een resultaat dat zich in minder dan 5% van de gevallen toevallig zal voordoen. (De z-waarde is 2, twee keer de standaardafwijking.) Om succes te boeken bij een parapsychologisch experiment hoeft de PK-kracht dus niet zo sterk en trefzeker te zijn.
Niets wijzer
We gaan er als vanzelfsprekend vanuit dat een dobbelsteen geen voorkeur heeft voor een van de zes zijden. Dit geldt echter lang niet voor elke dobbelsteen. Als de zes wordt aangegeven door zes kuiltjes in het hout, dan zal de steen aan die zijde iets lichter zijn dan aan de andere kant, waar slechts één stukje hout ontbreekt. Hij valt daardoor iets vaker op 6 dan op 1. Omdat je er nooit zeker van kunt zijn dat een dobbelsteen helemaal perfect is (en dat ook blijft), is het niet verstandig om proefpersonen louter de opdracht te geven zoveel mogelijk zessen te gooien. Alle zijden dienen even vaak aan bod komen.
Er zijn nog een aantal andere voorwaarden waaraan een betrouwbaar dobbelsteenexperiment moet voldoen. Je moet er zeker van kunnen zijn dat alle worpen correct genoteerd worden en dat er geen uitkomsten worden weggelaten. Het aantal worpen moet ook van tevoren worden vastgesteld. Anders zou je kunnen stoppen op een gunstig moment, wanneer de score net toevallig een piek heeft bereikt. Bovendien dienen de dobbelstenen bij voorkeur niet met de hand te worden gegooid, maar met behulp van een mechanisch apparaat.
Dean Radin en Diane Ferrari (1991) publiceerden een meta-analyse van 148 experimenten met dobbelstenen. Deze experimenten waren in de voorafgaande halve eeuw in vaktijdschriften gerapporteerd. Er waren in totaal 52 onderzoekers bij betrokken en er werden ruim tweeënhalf miljoen worpen geregistreerd. Bij 65 experimenten (44%) werd significant boven de kansverwachting gescoord, terwijl je minder dan 5% mag verwachten als alleen het toeval een rol zou spelen.
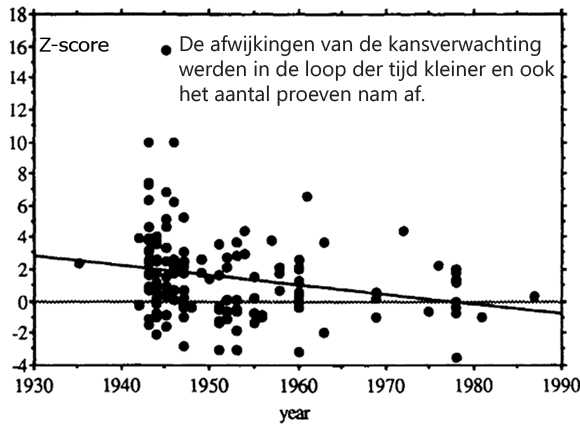
In de onderstaande grafiek is te zien dat vooral de eerste jaren veel proeven met hoge scores opleverden, terwijl er onder de laatste 16 experimenten nog maar 3 waren met een significant positief resultaat. In de jaren 1960 nam de belangstelling voor dit soort proeven sterk af en ook de resultaten liepen terug. Dat was nadat de psycholoog Edward Girden in 1962 een lang artikel publiceerde waarin hij kritiek leverde op de kwaliteit van het onderzoek. Hij merkte onder meer op dat onderzoekers soms geneigd waren hun hypothese te veranderen of na afloop subgroepen te creëren wanneer de uitkomsten niet in de gewenste richting gingen.
Radin en Ferrari gingen na in hoeverre de experimenten voldeden aan eisen van betrouwbaarheid. Daaruit bleek dat de kwaliteit in de loop van de jaren vooruit was gegaan. De meest succesvolle experimenten hadden doorgaans ook de meeste gebreken. Er waren slechts 69 experimenten (een minderheid) waarbij men alle zijden van de dobbelsteen even vaak als doelwit had gebruikt. Daarvan leverden 23 (een derde) een significant resultaat op. Omdat de gemeten effecten sterk varieerden, werden er nog tien uitschieters (positief en negatief) geëlimineerd. De overgebleven 59 proeven leverden samen nog steeds een significant effect op (z=2,6), al was dat veel kleiner dan wanneer je alle proeven meetelt (z=19,6).
Het lijkt aannemelijk dat veel dobbelproeven onbekend zijn gebleven omdat ze niet in tijdschriften werden gepubliceerd. J.B. Rhine, die vanaf 1937 hoofdredacteur was van het Journal of Parapsychology, wilde al bij voorbaat geen negatieve resultaten in zijn blad afdrukken, want daar werd de parapsychologie volgens hem niets wijzer van. Dit beleid werd pas in 1975 gewijzigd. Als we de eerder genoemde 59 gepubliceerde proeven zouden aanvullen met 60 ongepubliceerde proeven zonder resultaat (z=0), dan zou het geheel niet meer significant zijn (Bösch et al., 2006). Het is heel goed mogelijk dat er nog wel meer resultaten in bureauladen zijn blijven liggen. Daarom leveren de dobbelexperimenten geen sterk bewijsmateriaal voor het bestaan van psychokinese.
Radioactieve toevalsgetallen
De Britse parapsycholoog John Beloff (1920–2006) was in 1961 de eerste die samen met een natuurkundestudent onderzocht of mensen in staat zijn om invloed uit te oefenen op de deeltjes die door een radioactief preparaat worden uitgezonden. Maar de dertig proefpersonen die aan het experiment deelnamen, slaagden er niet in om de scintillatieteller (vergelijkbaar met een geigerteller) meer of minder deeltjes te laten tellen dan kon worden verwacht. Beloff boekte sowieso bijna nooit succes als experimentleider, waardoor hij bekend kwam te staan als een ‘psi-inhibitory experimenter’, een onderzoeker met een remmende invloed op paranormale effecten. Ook de studenten die hij opleidde aan de Universiteit van Edinburgh kregen daar vaak last van.
De Amerikaanse (in Duitsland geboren) fysicus Helmut Schmidt was een tegenpool van Beloff, want hij rapporteerde dertig jaar lang bijna uitsluitend geslaagde experimenten. Aan het eind van de jaren 1960 construeerde Schmidt een toevalsgenerator die gebaseerd was op radioactief verval. In het Engels noemt men het een Random Number Generator, RNG. Schmidt voerde er aanvankelijk experimenten mee uit waarbij de proefpersoon de toevalsuitkomsten moest voorspellen. Maar in 1970 schakelde hij over naar psychokinese: de proefpersonen moesten proberen de uitkomsten in een bepaalde richting te sturen.
Schmidts RNG bevatte een geigerteller en een elektronische oscillator die heel snel heen en weer sprong tussen twee posities, 0 en 1. Op het moment dat de geigerteller een elektron (bètadeeltje) registreerde dat door een radioactieve stof (strontium-90) werd uitgestoten, kwam de oscillator automatisch tot stilstand, zodat de uitkomst 0 of 1 was. Het is natuurkundig gezien onmogelijk om te bepalen op welk moment een bètadeeltje zal zal worden uitgezonden. Het gekozen getal was naar het scheen louter afhankelijk van het toeval.
De toevalsuitkomst werd zichtbaar gemaakt door middel van lampjes. De proefpersoon keek naar een cirkel van negen (of meer) lampjes, waarvan er telkens één brandde. Iedere keer dat de oscillator bij 0 of 1 tot stilstand kwam, ging het brandende lampje uit en een naastgelegen lampje aan. De lichtjes draaiden met de klok mee als de RNG een 1 produceerde en tegen de klok in als de uitkomst een 0 was (al werd dat soms omgedraaid). De proefpersonen moesten proberen om de lichtjes rond te laten draaien in een van tevoren gekozen richting. In feite moesten ze dus meer enen dan nullen produceren, of omgekeerd. Het aantal nullen en enen werd automatisch geregistreerd. Elke afzonderlijke proef duurde ongeveer twee minuten en daarbij versprongen de lampjes 128 keer.
Bij het eerste experiment dat Schmidt in 1970 rapporteerde, werden er in totaal 32.768 toevalsgetallen gegenereerd (256 keer 128). Je mag verwachten dat de helft van deze getallen de lampjes in de gekozen richting deed verspringen, maar het waren er 302 minder. De proefpersonen scoorden onder de kansverwachting (49 in plaats van 50 procent). Als de RNG daadwerkelijk zuivere toevalsgetallen leverde, dan zou zo’n afwijking niet vaker dan 1 op de 1000 keer voorkomen. Er leek dus iets bijzonders aan de hand te zijn.
Een mogelijke verklaring is, dat de RNG niet goed werkte. Schmidt vermeldde dat hij zijn RNG had getest door ’s nachts zeer lange reeksen toevalsgetallen te produceren. Daarbij waren geen afwijkingen aan het licht gekomen. Dit sluit echter niet uit dat de RNG soms tijdelijk van slag was, bijvoorbeeld alleen tijdens een opwarmperiode. Het is daarbij relevant om te weten dat de proefpersonen altijd eerst met het apparaat mochten oefenen. Pas wanneer ze het gevoel hadden dat het goed liep, werd de proef officieel gestart. Vaak mochten ze ook deels zelf bepalen hoelang ze doorgingen. Het is mogelijk dat ze onbewust gebruikmaakten van tijdelijke afwijkingen van de RNG (Alcock, 1990).
Een kat in een koud schuurtje
Schmidt veronderstelde dat je een toevalsproces doelgericht kunt beïnvloeden wanneer je de uitkomsten op de een of andere manier kunt waarnemen, in dit geval door naar de lampjes te kijken. Daarbij maakt het niet uit hoe de toevalsgebeurtenissen ontstaan. De proefpersonen hoeven niet te weten hoe de RNG functioneert en ook niet waar het apparaat zich bevindt. Ze hoeven zich slechts te concentreren op de uitkomsten om deze te kunnen beïnvloeden. Wie niet kan zien wat een RNG heeft gekozen, kan daar volgens Schmidt ook geen invloed op uitoefenen. Bij een van zijn experimenten gebruikte hij twee verschillende RNG’s, een simpele en een gecompliceerde. Zonder dat de proefpersonen dit wisten, schakelde hij tijdens de proef van de ene naar de andere RNG over. Dat had volgens hem geen nadelige invloed op de resultaten.
Men zou ervoor kunnen zorgen dat een RNG telkens twee toevalsgetallen produceert. Een van beide getallen wordt aselect gekozen om te worden gebruikt voor het experiment. Dit getal wordt op de een of andere manier zichtbaar gemaakt, terwijl het andere getal wordt opgeslagen in het geheugen van een computer en als controle fungeert. Je kunt dan nagaan of alleen de uitkomsten die door de proefpersoon worden bekeken, van de kansverwachting afwijken – zonder dat dit eveneens voor de controlereeks geldt. Op deze manier kun je controleren of de RNG tijdens het experiment naar behoren functioneert. Als er met de controlegetallen niks bijzonders aan de hand is, dan is er waarschijnlijk niks mis met het apparaat.
Helaas heeft Schmidt zulke controles niet uitgevoerd. Hij werkte met verschillende soorten RNG’s, maar vertelde in veel gevallen niet hoe hij de betrouwbaarheid daarvan op de proef had gesteld. Schmidt kreeg ook kritiek omdat zijn experimenten zo sterk van elkaar verschilden. Zo publiceerde hij kort na zijn lampjesproef een experiment waarbij een kat werd opgesloten in een koud schuurtje. De kat kon zich warmen aan een gloeilamp die was gekoppeld aan een RNG. Het was de vraag of het dier ervoor kon zorgen dat de lamp extra vaak ging branden. De eerste vijf proeven leverden samen een significant resultaat op, maar bij de resterende vijf brandde de lamp iets minder vaak dan verwacht mocht worden. Het was onduidelijk waarom Schmidt niet alle proeven bij elkaar optelde. Bij zijn volgende experiment onderzocht hij of kakkerlakken er op paranormale wijze voor konden zorgen dat ze minder vaak een stroomstoot kregen. Tot zijn verrassing leken ze de schokken lekker te vinden, want ze kregen er meer dan verwacht.
Schmidt bouwde meestal niet voort op eerdere successen, maar voelde om de een of andere reden de behoefte steeds wat nieuws uit te proberen. Soms waren zijn experimenten zo gecompliceerd dat men zich kon afvragen of hij de opzet wellicht pas gaandeweg had bedacht. Hij was vrijwel altijd de enige auteur van zijn onderzoeksartikelen, en soms ook een van de proefpersonen. Zijn verslagen lieten veel vragen open en hij was niet scheutig met aanvullende informatie.
Het kwam regelmatig voor dat proefpersonen tijdens de voorbereidende fase een resultaat boekten dat tegengesteld was aan het doel dat ze zich hadden gesteld. In zo’n geval moesten ze proberen om ook bij de officiële test het beoogde doel te missen, wat een nogal paradoxale opdracht is. Bij een proef die Schmidt in New Scientist (24 juni 1971) publiceerde, scoorde de ene proefpersoon 160 treffers boven de kansverwachting en de andere 144 onder de verwachting. Deze proef zou niet succesvol zijn geweest wanneer hij alle treffers bij elkaar op had geteld. Maar volgens hem hadden beide proefpersonen het gestelde doel bereikt, waardoor het totaal extreem significant werd (p<0,0000001).
Je zou kunnen vermoeden dat Schmidt het niet zo nauw nam met de waarheid. Er zijn echter nooit critici of collega’s geweest die hem van bedrog hebben beschuldigd. Dat zou ook niet verstandig zijn, want er zijn geen concrete aanwijzingen voor. We kunnen ons beter beperken tot de vaststelling dat de kwaliteit en betrouwbaarheid van Schmidts RNG-experimenten meestal te wensen overliet. Daar komt bij dat revolutionaire resultaten, die niet passen in het gevestigde natuurwetenschappelijke wereldbeeld, pas kunnen worden erkend wanneer ze in voldoende mate door andere wetenschappers worden bevestigd.
597 RNG-experimenten
Schmidt kreeg behoorlijk veel navolgers, mede omdat RNG-experimenten diverse praktische voordelen bieden. Je kunt ze makkelijk en goedkoop op een pc uitvoeren, waarbij de proefpersoon louter naar een beeldscherm hoeft te kijken en alle gegevens automatisch worden vastgelegd. Een geigerteller is niet meer nodig, want je kunt evengoed een RNG gebruiken die op thermische ruis werkt en die je rechtstreeks in je computer kunt pluggen.
Dean Radin en Roger Nelson, twee Amerikaanse (para)psychologen die verbonden waren aan de Princeton University, publiceerden in 1989 een overzicht van 597 RNG-experimenten. Hun artikel verscheen in Foundations of Physics, een vaktijdschrift over controversiële natuurkunde, en leek aan te tonen dat Schmidts resultaten herhaalbaar waren. Er waren in totaal 66 proefleiders bij de experimenten betrokken. Volgens Radin en Nelson zouden er 54.000 mislukte experimenten nodig zijn om het gemeten effect naar het kansniveau terug te brengen. Het gemiddelde scoringspercentage bedroeg 50,9 procent en de z-score was gemiddeld 0,65 in plaats van 0. (De z-score geeft aan hoeveel standaardafwijkingen het resultaat van de verwachtingswaarde ligt.) Er werden geen aanwijzingen gevonden dat de kwaliteit van de experimenten van invloed was op de resultaten of dat het succes aan slechts enkele onderzoekers te danken was. In 2003 publiceerden beide onderzoekers een update, die eveneens gunstig uitviel.
De laatste jaren verschenen er enkele kritieken op het werk van Radin en Nelson. Martin Schub (2006) wees erop dat de helft van de RNG-onderzoekers nooit een statistisch significant resultaat had gevonden. Bovendien waren 284 experimenten (bijna de helft) uitgevoerd in het laboratorium van Robert Jahn, de decaan van de School of Engineering van de Princeton University. De resultaten van deze proeven waren lang niet allemaal te vinden in de rapporten die Jahn publiceerde, maar Roger Nelson kon ze blijkbaar bemachtigen omdat hij bij het lab werkte. Radin en Nelson brachten ze in hun update terug tot één datapunt.
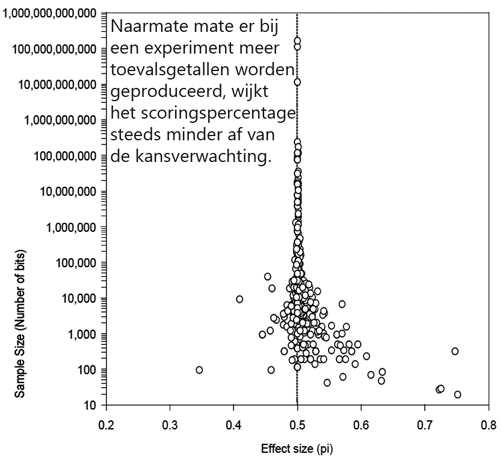
Schub vond het vreemd dat het scoringspercentage zakte naarmate men de RNG meer bits (nullen en enen) liet produceren. Als een RNG bijvoorbeeld 10.000 bits levert, waaronder 5100 enen (51%), dan bedraagt de z-score 2. Bij een experiment met tien keer zoveel bits (100.000) en hetzelfde scoringspercentage (51%), zou de z-score 6,3 bedragen. De z-scores van omvangrijke experimenten lagen echter niet hoger dan die van kleine studies, omdat het scoringspercentage in het eerste geval beduidend lager was.
Als je alle gegevens van de experimenten bij elkaar optelt, dan kom je volgens Schub uit op een scoringspercentage van 50,016 – veel lager dan de 50,9 procent die Radin en Nelson noemden. Dat kwam doordat zij van elk experiment de effectgrootte bepaalden en van deze waarden het gemiddelde berekenden. Daarbij hielden ze geen rekening met de omvang van een experiment. Alle resultaten wogen even zwaar mee. Soms wisten ze niet hoeveel toevalsgetallen er bij een experiment waren gebruikt. In dat geval stelden ze het aantal voor het gemak op 1, wat ongewenste statistische gevolgen had.
Het was volgens Schub mogelijk dat veruit het grootste deel van de experimenten nooit werd gepubliceerd omdat deze experimenten geen significant resultaat hadden opgeleverd. Je mag verwachten dat de gemiddelde z-score van de ongepubliceerde studies onder 0 ligt, omdat de beste resultaten daar niet meer tussen zitten. Volgens Schub waren er 2681 van zulke ongepubliceerde studies nodig om de boel weer in evenwicht te trekken – veel minder dan de 54.000 die Radin en Nelson berekenden, mede omdat zij daarbij uitgingen van een z-score van 0.
Schub had het idee dat de kwaliteit van de experimenten nogal laag was. In de onderzoeksverslagen werd meestal geen melding gemaakt van allerlei nuttige controlemaatregelen. Stel dat een RNG soms door een mankement een hele reeks enen achterelkaar produceert. Dat kun je eenvoudig voorkomen door ervoor te zorgen dat elk tweede getal automatisch in het tegendeel wordt veranderd (111111… wordt dan 101010…). In slechts 12% van de gevallen rapporteerden de onderzoekers dat ze dit hadden gedaan.
Radin et al. (2006a) vonden de meeste kritiek onterecht. Zo mag je volgens hen niet verwachten dat het scoringspercentage onafhankelijk is van het aantal bits dat men probeert te beïnvloeden. Je moet ook rekening houden met psychologische factoren en met het aantal bits dat per tijdseenheid wordt aangeboden. De ene RNG kan binnen een minuut wel honderd keer zoveel toevalsgetallen produceren als een andere. Wanneer een proefpersoon geen tijd heeft om zich op iedere uitkomst volledig te concentreren, dan wordt het PK-effect mogelijk kleiner.
Dean Radin erkende dat er meer RNG-experimenten zijn uitgevoerd dan we weten, omdat ze niet allemaal werden gepubliceerd. Het ligt voor de hand dat de ongepubliceerde proeven zelden succesvol waren. Radin acht het echter uitgesloten dat er een paar duizend experimenten in bureauladen zijn blijven liggen. In totaal telde hij niet meer dan 90 onderzoekers die zich met RNG-experimenten hadden beziggehouden. Als die elk tien experimenten verzwegen hebben, dan kom je nog niet boven de duizend. Radin vroeg het na bij collega’s, die hem meestal vertelden dat ze hoogstens één experiment hadden achtergehouden.
De experimenten waren naar het oordeel van Radin doorgaans van goede kwaliteit. Hij vond dat critici te hoge eisen stelden en er waarschijnlijk al bij voorbaat vanuit gingen dat een perfect experiment niets zou opleveren. Mocht er wel een positief resultaat uitkomen, dan is dat voor de ongelovigen slechts een reden om te veronderstellen dat er blijkbaar ergens iets mis is gegaan. Dat kunnen ze altijd blijven volhouden, want het perfecte experiment bestaat niet. Ongeloof kan zo onredelijk en dogmatisch worden dat men zich niets meer van de feiten aantrekt. Maar het is overdreven om te beweren dat het al zover is en dat de bewijzen zo sterk zijn dat je ze alleen tegen beter weten in kunt negeren. Zo was het zeer teleurstellend dat Jahn (2000) er niet in slaagde om zijn resultaten in samenwerking met twee Duitse onderzoeksteams te repliceren.
Dalende lijn
In 2006 verscheen in Psychological Bulletin een nieuwe meta-analyse van 380 RNG-experimenten, waarbij de proefpersonen hadden geprobeerd doelgericht toevalsgetallen te beïnvloeden. De analyse was een onderdeel van de dissertatie van de Duitse parapsycholoog Holger Bösch, die samenwerkte met een Engelse en een Duitse collega. De onderzoekers verzamelden alle experimenten die aan hun selectiecriteria voldeden, waaronder 93 congresbijdragen en rapporten die niet in tijdschriften waren verschenen.
In totaal waren er 83 studies (22%) die een significant effect opleverden in de gewenste richting, en 23 studies (6%) die een significant negatief effect vertoonden, tegengesteld aan het doel. Iets meer dan de helft van de experimenten werd in de jaren 1970 uitgevoerd. Van de experimenten uit de periode voor 1975 leverde 47 procent een positief resultaat op, terwijl dat bij slechts 13 procent van de latere experimenten het geval was. Het was opvallend dat de effecten die werden gemeten zeer sterk varieerden.
Het gemeten effect was doorgaans het grootst bij de kleinste experimenten. Dit waren vaak tevens de oudste experimenten, die het minst zorgvuldig waren opgezet. Je zou kunnen veronderstellen dat RNG-onderzoekers meestal niet de moeite namen om een kleine studie te rapporteren wanneer deze niets opleverde. In zo’n geval gingen ze wellicht liever meteen door met een volgend experiment of ze stopten ermee. Bij 19 procent van de proeven werden maximaal duizend toevalsgetallen gebruikt, bij 53 procent maximaal tienduizend en bij 12 procent meer dan een miljoen. Naarmate het aantal toevalsgetallen toenam, zakte de effectgrootte geleidelijk naar nul. De drie grootste proeven leverden merkwaardig genoeg zelfs een significant negatief resultaat op, al week het scoringspercentage nauwelijks nog af van de kansverwachting (het was circa 49,998%).
Er waren ook experimenten (30%) waarbij men onderzocht in hoeverre bepaalde psychologische factoren van invloed waren op het resultaat. Maar omdat de afwijkingen van de kansverwachting sowieso erg klein en zeer wisselvallig waren, leverden zulke analyses niks op. De resultaten werden gewoonlijk beter wanneer de onderzoekers hun gegevens in twee of meer subgroepen verdeelden. Maar in dat geval moet je er wel zeker van kunnen zijn dat ze die indeling al hadden bedacht voordat ze de resultaten kenden.
Op basis van een zogenoemde Monte Carlo-simulatie stelden Bösch et al. (2006) vast dat er 1544 ongepubliceerde, mislukte experimenten nodig waren om de gevonden afwijking van de kansverwachting teniet te doen. Tegenover elk experiment dat ze in hun verzameling hadden opgenomen, zouden er dus nog vier moeten zijn die onbekend waren gebleven en die slechts toevalsresultaten opleverden. Dan kun je het gemeten effect verklaren, zelfs zonder dat je hoeft aan te nemen dat er bij sommige proeven iets mis is gegaan. De drie kritische parapsychologen vinden dit aantal niet ondenkbaar, omdat een RNG-experiment niet veel tijd hoeft te kosten. Ze kunnen zich ook wel voorstellen dat experimenten soms halverwege werden afgebroken. De Nederlandse parapsycholoog Dick Bierman merkte ooit op dat het bij een modern RNG-experiment gemiddeld ongeveer 1000 seconden kost om alle data te verzamelen.
Bösch, Steinkamp en Boller adviseren hun collega’s om in het vervolg alle beoogde experimenten van tevoren ergens aan te melden, compleet met de wijze waarop men de resultaten na afloop wil berekenen. Dat is al langer gebruikelijk bij medische proeven. Pas als je een complete verzameling proeven kunt analyseren, kun je nagaan hoeveel succes er werkelijk is geboekt. De RNG-experimenten leveren naar het schijnt nog steeds te veel op om ze als irrelevant terzijde te kunnen schuiven. Maar de effecten zijn zo klein en lopen zo sterk uiteen, dat je er geen duidelijke conclusies uit kunt trekken. De parapsychologie is dus zoals gebruikelijk nog niet veel verder gekomen.
Literatuur
Alcock, James E. (1990). Science and supernature. Buffalo, New York: Prometheus Books.
Bösch, Holger, Fiona Steinkamp en Emile Boller (2006). Examining psychokinesis: the interaction of human intention with random number generators – a meta-analysis. Psychological Bulletin, 132(4), 497-523.
Bösch, Holger, Fiona Steinkamp en Emile Boller (2006). In the eye of the beholder. Psychological Bulletin, 132(4), 533-537.
Jahn, Robert et al. (2000). Mind/Machine Interaction Consortium: PortREG Replication Experiments. Journal of Scientific Exploration, 14(4), 499-556.
Radin, Dean & Diana C. Ferrari (1991). Effects of consciousness on the fall of dice: A meta-analysis. Journal of Scientific Exploration, 5(3), 61-84.
Radin, Dean, Roger Nelson, York Dobyns en Joop Houtkooper (2006a). Assessing the evidence for mind-matter interaction effects. Journal of Scientific Exploration, 20(3), 361-374.
Radin, Dean, Roger Nelson, York Dobyns en Joop Houtkooper (2006b). Reexamining psychokinesis: comments on Bösch, Steinkamp, and Boller (2006). Psychological Bulletin, 132(4), 529-532.
Schub, M.H. (2006). A critique of the parapsychological random number generator meta-analyses of Radin and Nelson, Journal of Scientific Exploration, 20(3), 402-419.
Uit: Skepter 22.2 (2009)