door Jan Willem Nienhuys (22/11/2010)
Tegenwoordig hoort men vaak de Evidence Based Medicine (EBM) ophemelen. Maar die is nog niet goed genoeg. De Science-Based Medicine (SBM), zeg maar natuurwetenschappelijke geneeskunde, is een poging om een duidelijk zwak punt van EBM te repareren. Ondertussen stelt een beroemd artikel (Why Most Published Research Findings Are False, 2005) van de Grieks-Amerikaanse epidemioloog John P.A. Ioannidis (foto), onlangs besproken in The Atlantic (Lies, Damned Lies and Medical Science) dat heel veel resultaten van medisch onderzoek, dus van die hooggeroemde EBM, fout zijn.
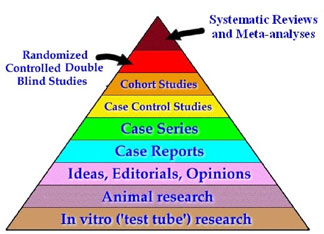
In de EBM wil men deugdelijke bewijzen hebben voor medische behandelingen. Er zijn verschillende graden van deugdelijkheid. Bijna bovenaan staat het bewijs door middel van een dubbelblinde proef met loting en controlegroep, in het Engels: randomized controlled trial (RCT). De eenvoudigste opzet is dat men een groep zieke personen in tweeën splitst: de ene helft krijgt de te onderzoeken behandeling, en de andere helft krijgt een geloofwaardig en ethisch verantwoord alternatief, bijvoorbeeld een neppil of een bekend werkend middel. De bedoeling is dat noch de behandelaar, noch de zieke weet of zelfs maar kan raden wie wat krijgt, want anders krijg je allerlei ongewenste effecten. Daarom moet ook door loting worden bepaald wie in welke groep terecht komt.
Nog hoger dan het RCT staat een systematisch overzicht van veel RCT’s. Een stuk lager dan een RCT staat bijvoorbeeld een case series: een verslag van wat er met een aantal behandelde patiënten gebeurd is, dus zonder controlegroep, en ook niet geblindeerd.
Tegen deze EBM zijn twee bezwaren. Het eerste bezwaar, dat van Ioannidis, is dat die RCT’s toch veel foute resultaten opleveren. Het tweede bezwaar is dat deze EBM sterk gericht is op het vinden van een bewijs voor werkzaamheid, en dat in de EBM-filosofie nauwelijks wordt gekeken naar wat er aan tegenbewijzen beschikbaar is. Aangezien in het ideaalbeeld van de natuurwetenschap weerleggingen of pogingen daartoe een belangrijke rol spelen, doet de sterke nadruk op bewijzen zoeken onwetenschappelijk aan. Er zijn nog andere bezwaren tegen de heiligverklaring van de RCT (hoe zou je zo de werkzaamheid van parachutes moeten aantonen?), maar daar wil ik het nu niet over hebben.
Cyanide, chelatie, homeopathie
Een voorbeeld is het onderzoek naar Laetrile. In 1982 verscheen in het New England Journal of Medicine een verslag van hoe het gegaan was met 178 patiënten met kanker die het middel Laetrile kregen. Laetrile is eigenlijk een vorm van blauwzuur (cyanide), een zwaar vergif. In geen enkel opzicht bleken de patiënten erop vooruit te zijn gaan, en diverse patiënten vertoonden verschijnselen van cyanidevergiftiging; sommigen hadden vrijwel dodelijke doses cyanide in hun bloed. Hoewel dit geen RCT was, kun je toch wel zeggen dat hiermee Laetrile had afgedaan. Toch werd er nog in 2006 een systematic review over Laetrile gepubliceerd. Laetrile is niet het enige voorbeeld.
Van chelatietherapie is ook afdoende aangetoond dat het niets helpt en nog gevaarlijk is bovendien. Niettemin is er in de VS nog onlangs een RCT opgestart (TACT) om na te gaan of chelatietherapie werkt. De werving van patiënten is een tijdlang gestaakt in verband met aantijgingen van onregelmatigheden. Later zijn ze weer hervat, en nu is het wachten op de einduitslag. Men kan er tamelijk zeker van zijn dat bij de te verwachten negatieve uitslag de chelatiebehandelaars hun praktijken niet zullen stoppen. Waar de reguliere geneeskundigen zich vaak wel wat aantrekken van een negatieve uitslag, is de bereidheid dit te doen afwezig bij de alternatieve.
Een ander voorbeeld is homeopathie. Hoewel sommige homeopathische middelen eigenlijk nauwelijks verdunde kruidenpreparaten zijn, en het publiek ook vaak denkt dat homeopathie een soort kruidengeneeskunde is, zijn de echte homeopathische middelen zo sterk verdund dat ze niet kunnen werken. De behandelingsvoorschriften bij de homeopathie berusten op allerlei subjectieve verschijnselen die zulke hoogverdunde middelen bij gezonde mensen zou hebben veroorzaakt, met andere woorden, op fantasie. Basiskennis van de natuurwetenschap volstaat om het oordeel te vellen dat verder onderzoek niet meer nodig is. Dit maakt geen indruk op het Amerikaanse instituut voor onderzoek van alternatieve geneeskunde. Dat subsidieerde zelfs een meerjarig universitair onderzoek dat met qEEG probeerde vast te stellen wat er in de hersenen gebeurt bij mensen die homeopathische middeltjes hadden ingenomen.
Het feit dat homeopathie eigenlijk te onzinnig voor woorden is, is al lang geleden besproken door bijvoorbeeld Kleijnen, Knipschild, en Ter Riet (1991) en Vandenbroucke (1998-2000). Vandenbroucke schreef: ‘Stel dat dit [overzicht van RCT’s] niet ging over homeopathie, … [dan] … zouden we zeggen dat … er een duidelijk effect was.’ Kleijnen et al. maken een soortgelijke opmerking: ‘Based on this evidence we would be ready to accept that homoeopathy can be efficacious, if only the mechanism of action were more plausible.’ In plaats dat de homeopaten beschaamd hun mond houden tot de basis van hun toverij goed gegrondvest is in de natuurwetenschap, kraaien ze het uit dat gerenommeerde onderzoekers ook zeggen dat homeopathie eigenlijk bewezen is. Sterker nog, men lijkt zich te beklagen over discriminatie en meten met twee maten, dat allerlei reguliere behandelingen wel erkend worden en de homeopathie, met even veel bewijs notabene, nog steeds niet.
Piramide
De voorstanders van de natuurwetenschappelijke geneeskunde (SBM) vinden dat de natuurwetenschap wat serieuzer genomen moet worden. Een belangrijke groep pleitbezorgers van de EBM werkt samen in de zogeheten Cochrane Collaboration. Deze groep publiceert regelmatig systematische overzichten van wat er op allerlei medisch gebied is onderzocht. Die groep heeft bijvoorbeeld ook in alle ernst enkele RCT’s van het onzinmiddel Oscillococcinum betrokken in een systematisch overzicht. De EBM’ers erkennen wel de waarde van basiskennis van de natuurwetenschap, maar die staat op de laagste plaats. Dat is correct wanneer men alleen maar denkt aan ‘bewijzen dat een medicijn werkt’. Met de wet van behoud van energie komt men niet zo ver bij de ontwikkeling van werkzame behandelingen. Helemaal nutteloos is die wet niet, want die suggereert dat minder eten en meer bewegen helpt tegen obesitas.
In de praktijk speelt basiskennis indirect wel een rol, want RCT’s zijn duur. Subsidieverstrekkers accepteren alleen de allerbeste onderzoeksvoorstellen. Onderzoekers die aan een RCT willen beginnen, en niet kunnen beredeneren dat ze enige kans van slagen hebben, zien hun voorstel meestal de prullenbak ingaan.
Speciaal op het gebied van de alternatieve geneeskunde is er echter veel waarvoor de basisveronderstellingen zo mal zijn, dat een onderzoek vergelijkbaar zou zijn met een onderzoek naar de werking van een perpetuum mobile of piramidekrachten.
De SBM’ers vinden dus dat argumenten van aannemelijkheid vooraf een belangrijker rol moeten spelen. Men zou ook kunnen zeggen dat de EBM-piramide van onderaf beklommen moet worden, en dat wie een bepaalde trede niet haalt, uitgesloten dient te worden van de hogere stadia. Zo gaat het buiten de wetenschap ook: wie faalt als korporaal wordt geen generaal. Maar zoals men ziet, staat er bij de onderste trede van de piramide niet: basic science laws.
Odds vooraf en achteraf
Het bezwaar van Ioannidis heeft ook te maken met aannemelijkheid vooraf. Om dat toe te lichten eerst een voorbeeld van een onderzoek naar een test voor de aanwezigheid van laten we zeggen een of andere genetische kenmerk. We nemen aan dat een op de negen mensen dat kenmerk bezit. De test is niet perfect. In slechts 80 procent van de gevallen zal die een aanwezig kenmerk aantonen. Bovendien, als iemand het kenmerk niet heeft, zal in 25 procent van de gevallen de test toch ten onrechte beweren dat het aanwezig is. (Voor kenmerk kan men ook enge ziekte denken, maar zo houden we het voorbeeld wat neutraler.)
Nu ondergaat iemand de test. Stel eens dat de test zegt ‘kenmerk aanwezig’. Voordat de betrokkenen de test onderging waren de odds op aanwezigheid van het kenmerk een tegen acht (1:8). Na een positieve uitslag zijn de odds anders, namelijk 2:5. Het rekenregeltje is eenvoudig: vermenigvuldig de vooraf-odds (1/8) met 80/25, dus met de verhouding ‘kans correct-positief’ : ‘kans fout-positief’, en het resultaat is de achteraf-odds (in deftig Latijn: a priori en a posteriori odds).
Valt de test negatief uit, dan moeten we de vooraf-odds vermenigvuldigen met de verhouding ‘kans op fout-negatief’: ‘kans correct-negatief’, dus met 20/75. De achteraf-odds zijn dan 1:30. We zien dus dat we het bekend worden van een testuitslag kan worden opgevat als een overgang van vooraf- naar achteraf-odds.
Misschien vindt u het rekenen met breuken vervelend. Ik kom zelf ook altijd in de war. Maar men kan bijvoorbeeld uitgaan van een populatie van 1125 personen, waarvan er 125 het kenmerk wel hebben, en 1000 niet. Als we ze allemaal testen, verwachten we: 100 correct-positief, 25 fout-negatief, 250 fout-positief, 750 correct-negatief. De verhouding 2:5 zien we dan terug als 100:250 en de verhouding 1:30 als 25:750.
We kunnen odds in kansen en vice versa omrekenen, maar de formules in termen van kansen zijn een stuk onsmakelijker. De factor waarmee vermenigvuldigd moeten worden noemen we de aannemelijkheidsverhouding of likelihood ratio (LR). In medische kringen noemt men het percentage correct-positief ook wel sensitiviteit en het percentage correct-negatief heet dan specificiteit.
Farmaceutisch bedrijf
Een wat ingewikkelder voorbeeld betreft een onderzoek naar een geneesmiddel tegen een ziekte X. Veronderstel dat bekend is dat zonder geneesmiddel 20 procent van de X-lijders beter wordt. Men vermoedt dat met het geneesmiddel 36 percent van de zieken beter wordt. Men besluit 100 zieken te behandelen met het nieuwe middel, en men neemt zich voor dat als er 28 of meer beter worden, verder te gaan met onderzoek van het middel, omdat het kennelijk toch iets doet. De reden voor het getal 28 zal aanstonds duidelijk worden.
Stel eens dat het middel eigenlijk helemaal niet werkt. Wat is dan, met deze getallen, de kans dat je toch stom toevallig 28 genezen patiënten krijgt, en dus volkomen ten onrechte denkt dat je middel zin heeft (een zogeheten fout van de eerste soort)? De waarschijnlijkheidsleer vertelt ons (reken, reken) dat als door de bank genomen, dus gemiddeld over zeer grote aantallen, 20 procent beter wordt, er een kans van 3,42% is dat in een groep van 100 er 28 of meer beter worden.
Het kan natuurlijk ook dat het middel wel werkt en dat die 36% genezing de goede waarde is, maar dat we alweer stom toevallig met deze groep van 100 de 28 genezen personen niet halen. Ook die kans (op een fout van de tweede soort) kunnen we uitrekenen (aangenomen dat die 36% klopt). Hij bedraagt 3,62%, met andere woorden, de kans dat een werkend middel ook goed wordt bevonden is 96,38%. Statistici noemen dit getal (dus die 96,38% in dit geval) het onderscheidingsvermogen (power) van de test.
Als u een farmaceutisch bedrijf runt, dan komen uw onderzoekers regelmatig met stofjes aanzetten waarvan ze om allerlei redenen (proeven in reageerbuizen enzo) denken dat het geschikte geneesmiddelen zouden kunnen zijn. Laten we zeggen dat zij en u uit ervaring weten dat slechts één op de honderd middelen echt blijkt te werken. Wat kunt u nu zeggen na afloop van zo’n test als boven? De vooraf-odds zijn 1:100. Dat is gewoon bedrijfsstatistiek. We testen nu niet op een of genetisch kenmerk, maar op de eigenschap ‘is werkzaam medicijn’. Wat zijn de achteraf-odds na een geslaagde test? Onze rekenregel van zonet geeft het antwoord. De verhouding ‘kans correct-positief’ : ‘kans fout-positief’ bedraagt nu 96,38 : 3,42, en de achteraf-odds zijn dus ongeveer 28 maal zo groot als de vooraf-odds, dus 28:100, met andere woorden er is nog een aanzienlijke kans (namelijk 28/128, is 22%) dat het middel eigenlijk niks doet, maar die kans is niet zo hoog als de 99% waar we mee begonnen.
De reden voor de grens van 28 is duidelijk: op die manier is de fout van de eerste soort ongeveer gelijk aan de fout van de tweede soort. Omdat de twee hypothesen (20 percent genezing en 36 percent genezing) zover uit elkaar lagen, kunnen we toe met slechts 100 proefpersonen. Toen Franse sceptici ruim twintig jaar geleden een test deden voor het Marseffect, hadden ze te maken met twee hypothesen die veel dichter bij elkaar lagen: 17 en 22 percent (het doet er hier niet toe wat de eigenschap in kwestie was). Ze hadden daarom minstens 1000 proefpersonen nodig om te zorgen dat de fouten van de eerste en tweede soort beide 2,5 procent waren, zodat wat de uitslag ook was, tenminste een van beide hypotheses zou sneuvelen.
Korrel zout
In de praktijk van het wetenschappelijk onderzoek gaat het echter helemaal niet zo. Het enige waar behoorlijk de hand aan wordt gehouden is dat men de kans op een positief nepresultaat (in geval het middel of de getoetste bewering onzin is) doorgaans onder de 5 procent probeert te houden. Dat is de beroemde p-waarde. Wat in het bovenstaande voorbeeld die 20% was, kent men ook vaak niet (die kan erg afhangen van de groep patiënten die belieft mee te doen aan de proef), dus men gebruikt een placebo-behandelde groep als vergelijkingsmiddel. Het onderscheidingsvermogen is vaak ook niet bekend. Dat kan men namelijk alleen uitrekenen als men de zogeheten alternatieve hypothese kent: een uitspraak over hoe groot het effect van het middel zou zijn als het werkte. Weet men niets over de effectgrootte, dan maakt men de wens de vader van de gedachte, en men kiest als gehoopt effect iets dat klinisch interessant is. Heeft men niet zo’n precieze alternatieve hypothese, dan kan men in alle redelijkheid verwachten dat áls het middel een klein beetje meer succes heeft dan een nepmiddel, dit in 50 procent van de gevallen bij een proef ook het geval zal blijken. De rekenregel vertelt ons dus dat je de achteraf-odds kunt verkrijgen uit de vooraf-odds, door bij een geslaagde proef (‘statistisch significant’) te vermenigvuldigen met 50/5, dus met 10. Bij een mislukte proef moet men dan vermenigvuldigen met 50/95, dus ongeveer delen door twee.
Dat houdt twee dingen in. In de eerste plaats doen de vooraf-odds er niet zo toe als we een flink aantal onberispelijke en positief uitgevallen RCT’s hebben. Als men een klein getal een flink aantal malen achter elkaar met 10 vermenigvuldigt, komt er doorgaans een groot getal uit. In de tweede plaats, als de vooraf-odds heel erg klein zijn (zo klein als de kans dat de gehele natuur- en scheikunde van de afgelopen 200 jaar met zijn miljoenen vaak zeer accurate proeven die elk jaar ook nog door beginnende studenten herhaald worden, het helemaal mis heeft) dan brengt zelfs een onberispelijk RCT daar geen verandering in.
Men zou kunnen zeggen dat dit de rationale is voor de stelling van de SBM: wat uiterst onaannemelijk is op basis van de bekende wetenschap, moeten we niet gaan onderzoeken, want dat is verspilling van moeite. Zelfs positief uitgevallen onderzoeken van iets dergelijks moeten we met een flinke korrel zout nemen. Het adagium ‘buitengewone beweringen vergen buitengewone bewijzen’ past ook in dit schema. Als we te maken hebben met een erg onaannemelijke bewering, dan zal een geslaagde test daarvoor ook een enorme likelihood ratio moeten hebben, corresponderende met laten we zeggen een p-waarde van 0,0000001.
Ioannidis legt in zijn beroemde artikel ook ongeveer het bovenstaande uit (maar in wat geleerdere taal). Hij wijst erop dat er in het geneeskundige onderzoek tal van praktijken bestaan waardoor speciaal de p-waarde niet is wat ze lijkt.
Rachmaninov
Immers in de bovengeschetste situatie ging het om een onderzoek waar van tevoren gepland was dat 100 personen onderzocht werden, en dat de grens lag bij 28. Voor elke persoon is het duidelijk of die beter is geworden of niet. Bij echte onderzoeken gaat het vaak om meerdere uitkomstmaten, bijvoorbeeld diverse scores op subjectieve vragenlijsten, of objectieve meetgegevens. Als je bijvoorbeeld kankerpatiënten registreert en ze de oren van het hoofd vraagt naar hun leefstijl is het heel gemakkelijk om bij elk van tien (of honderd) soorten kanker tien (of honderd) aspecten van de leefstijl (consumptie van kaas, koffie of belminuten) te testen en dan de ‘indrukwekkende verbanden’ er tussenuit te vissen. Men kan ook, als de patiënten zich een voor een melden, om de tien patiënten kijken of er al ‘significantie is bereikt’. Is dat het geval, dan houdt men op, en publiceert men. Valt na een betrekkelijk klein aantal het schijnbare effect erg tegen, dan stopt men met het onderzoek, en dan hoort men er nooit meer van. Het (achteraf) verwijderen van patiënten wil ook wel eens helpen. Zo bleek bij beschouwing van een groot aantal RCT’s de verumgroep systematisch kleiner te zijn (door uitval) dan de placebogroep.
Een andere truc is dat men allerlei subgroepen gaat analyseren, en dan toevalsvondsten daarin breed uitmeet. Door deze en andere fouten kan de werkelijke p-waarde flink boven de gerapporteerde waarde in het artikel oplopen. Ook nadat een onderzoek opgeschreven is, blijven selectie-effecten doorwerken. Met ‘vier koppen koffie dagelijks doet de kans op ziekte Y significant toenemen’ (of ‘afnemen’) heeft men een flinke kans op publicatie, terwijl men met ‘het houden van katten heeft geen invloed op darmkanker’ of ‘luisteren naar muziek van Rachmaninov heeft geen invloed op epilepsie (of hoofdroos)’ natuurlijk geen tijdschriftredactie zo gek krijgt dat af te drukken, tenzij een mafkees eerder net andersom had beweerd. Het bovengenoemde Marseffect wás trouwens zo’n idiote veronderstelling en werd alleen maar getest omdat de bedenker ervan beweerde dat hij heel veel experimenteel bewijs had.
Ioannidis betoogt dat het soort beweringen waarover publicaties verschijnen van een type zijn waarvoor de vooraf-odds heel laag zijn. Speciaal in de genetica zijn de vooraf-odds van verbanden tussen genetische kenmerken en ziektes extreem klein. Voor de hand liggende beweringen als ‘roken veroorzaakt kanker’ zijn al uitgemolken, dus het onderzoek gaat vaak over dingen met lage vooraf-odds. Bovendien mankeert er zoveel aan de rapportage van onderzoeken dat deze waarschijnlijk een heel povere verhouding ‘kans correct-positief’ : ‘kans fout-positief’ hebben, en dat het dus eigenlijk niet verwonderlijk is dat men aan de lopende band verneemt dat het een of andere eerder gevonden ‘resultaat’ niet blijkt te kloppen.
Zo kan het gebeuren dat optimistische verhalen over het nut van vitamines (en meer recent visolie) moeten worden teruggetrokken, evenals die over het nut van de mammomobiel of Prozac. We hebben het dan maar niet over frauduleuze of incompetente onderzoeken zoals ‘bidden helpt bij IVF’ of ‘vaccinatie geeft autisme’. Ioannidis schat dat zelfs van de ‘goede’ RCT’s nog een kwart gewoon een fout resultaat oplevert.
Strikt genomen kan men meestal niet spreken van vooraf-odds voor zulke beweringen, omdat er geen experimenteel model denkbaar is waarmee men met benadering de kansen kan meten of schatten. Er is eigenlijk niet zoiets ‘de kans dat homeopathie werkt’. We kunnen geen serie universa uit een hoge hoed trekken (laat staan een representatieve steekproef uit de verzameling ‘alle’ universa) en in elk daarvan vaststellen of er wel of niet tussen 1800 en 2000 een belangrijk meetbaar spiritueel beginsel is gemist dat de homeopathie verklaart. Niettemin maakt de bovenstaande benadering duidelijk wat de rol is van de plausibiliteit vooraf bij het beoordelen van onderzoek.
In kringen van alternatieve genezers is men opgetogen over de mare dat de EBM niet deugt, en dat al de RCT’s toch allemaal fout zijn. Daar vreest men de RCT’s (behalve als ze een of andere alternatieve leer schijnen te bevestigen), en is men heel blij als afbreuk gedaan wordt aan de waarde van RCT’s. Maar waar mankeert er heel veel aan de onderzoeksmethodiek, en waar is de kritiek van Ioannidis speciaal van op toepassing? Dat is op het terrein van de alternatieve geneeskunde!
Oorspronkelijk was dit artikel gepubliceerd op het (oude) Skepsis-blog en bestond de mogelijkheid om daaronder in discussie te gaan, waar geregeld uitvoerig gebruik van werd gemaakt. De discussie onder dit bericht kan de geïnteresseerde teruglezen in deze pdf (13 pagina’s).