Cars need gasoline and a washing machine will stop running the moment you pull the plug. This is because energy can be converted from one form to another, but it cannot be made to magically appear out of nothing. Anyone making claims about an engine running without an energy input is either a swindler or an ignoramus. The ‘Rosch Thrust Kinetic Generator’ is the most recent attempt at hyping up a ‘free energy’ engine. Common sense and a little bit of high school physics are all that is needed to show that here too the Law of Conservation of Energy stands in way.
The device shown left is the Rosch Thrust Kinetic Generator. It is developed and manufactured in Serbia, but the company also has branches in Germany and in Switzerland. Google on Rosch Thrust Kinetic Generator and glossy brochures pop up, promising a bright new future (see for example the site of Zilverstroom).
How does it work? Or rather, how is it supposed to work? The entire device in the illustration above is submerged in a column of water. At the bottom on the left side of the device air bubbles are injected into the water column. These air bubbles are captured in containers. The containers are pushed upwards by the air and the engine’s chain transmission is set in motion. Once a container reaches the top of the water column, it topples and the side with the holes comes up. The injected air then escapes. The upward force only pushes up containers on the left side of the column and this is what keeps the system in motion. Combustion engines will be museum pieces. Windfarms will be mere monuments. Nuclear power will be obsolete.
Sounds too good to be true? That’s because it is. The rub is that it takes energy to pump air bubbles into the water column. The maximum amount of energy that can be extracted as the air bubbles push the containers upward equals exactly the amount of energy it takes to pump the bubbles into the water column.
What Is The Source Of The Energy?
Like everything in the universe, flowing gasses and moving liquids do not escape the Law of Energy Conservation.
As is demonstrated with the next illustration, it requires pressure, and therefore force and energy, to insert an air bubble at the bottom of the water column.

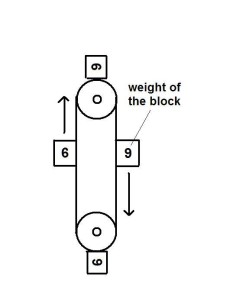
Let the mass of the water column be M. The insertion of the air bubble raises the level of the entire column by a height Δh. The energy that is necessary to do this is E = M × g × Δh, where g is the acceleration of gravity. M×g is the weight of the column of water, i.e. the force with which gravity is pulling it down. The height Δh is the distance that needs to be covered when expending energy to overcome gravity. When the inserted air bubble next moves up, the mass of water above the air bubble gets smaller and smaller. Effectively, the water is falling around the air bubble and that falling again releases the energy that was put into lifting up the entire column. When the air bubble reaches the surface and disappears, the water column is back in its original state. The Rosch Generator shown in the first figure captures the air bubbles in containers. The upward motion caused by the buoyant force is used to generate energy. In the impossible case that the device is completely frictionless and the energy conversion is 100% efficient, only in that case will the device produce exactly the amount of energy that is required to insert the air at the bottom of the column.
You can take a piece of styrofoam and push it down under water. When you next release that piece of styrofoam there, it will come to the surface. Energy can indeed be extracted from that upward motion in a way that is analogous to how a hydroelectric power plant extracts energy from falling water. However, the energy that is extracted from the upward motion of the styrofoam will never be larger than the energy it took to push the styrofoam down. If you don’t push the styrofoam straight down, but instead insert it at the bottom of the water column, you need just as much energy. This is because the water pressure that you have to work against in the insertion is directly proportional to the depth below the water surface. The second figure illustrates this.
Many “free energy” devices are boxes filled with electrical parts where it is hard to figure out what is happening or what is supposed to happen. Claiming that patent applications are still pending, the manufacturers of these devices also commonly refuse to have their devices or designs examined by outsiders. With such secrecy and vagueness it is impossible to have a meaningful discussion. But Rosch is remarkably open and forthright. The concept and the device are refreshingly simple. Because of this, we can also be short and concise when showing that it is all a mistake.
Quarter Of A Million Households

On the internet you’ll find stories about producing 100 megawatts (one hundred million watts!!!) and about how a power plant with a capacity like that can be commissioned. Apparently over at Rosch’s they think big. One hundred megawatts is roughly the at-home electrical power consumption of a quarter of a million West-European households all together. We are talking about powering a city here!
There are also smaller models for domestic use. These can be ordered in Germany from the “Verein Gaia” . The figure left is a photograph of such a model.
On the website of the Dutch “free energy” association FE4All (Free Energy for All) there is an almost touching description of how four members actually traveled to Germany to inspect this smaller device. But in the end frugality won the day as the quartet agreed that 15,000 euros (US$16,500) was a little too steep. Apparently even Holland’s most revolutionary innovators have to sometimes watch the pennies! But according to their website FE4All is seriously considering buying a Dutch license for the technology. Really … a license like that would be worth no more than the paper that it is printed on.

Geachte heer Bier,
Ik heb nog niet aan de opstelling gerekend, en waarschijnlijk heeft u volkomen gelijk dat het principe niet werkt. Echter ik heb wél een opmerking: in uw voorbeeld laat u een waterkolom met hoogte delta h naar boven gaan. Maar wat gebeurt er als “het systeem” zich in een “oneindig” grote zee bevindt? Dan is delta h = nul; het verplaatste water verplaatst zich dan zijwaarts hetgeen geen energie zou kosten (de beweging staat dan haaks op de zwaartekracht) als we wrijvingsverliezen op nul stellen.
Bovendien is er een tweede effect: De luchtbel wordt, naarmate hij naar boven gaat, steeds groter omdat de statische druk van het water naar boven afneemt. Aangezien water “onsamendrukbaar” is zal de soortelijke massa van water gelijk blijven en volgens Archimedes wordt dus de opwaartse druk steeds groter door het toenemende volume van de luchtbel.
Uw berekening is (volgens mij althans) een beetje kort door de bocht (maar nogmaals: of het principe werkt weet ik óók niet. Er zal eens écht aan gerekend moeten worden).
Als laatste opmerking: misschien ben ik heel dom, maar het axioma “energie wordt niet geboren” (zie de laatste regel van de eerste alinea) is achterhaald, evenals het feit dat een atoom ondeelbaar zou zijn en de zon om de aarde zou draaien. Immers Einstein heeft met zijn formule E = mc2 vastgelegd dat er wel degelijk energie kan worden “geboren”. Volgens mij: zelfs als gewoon hout wordt verbrand wordt er energie “geboren” middels conversie van massa in energie. Dat we het nooit hebben kunnen meten ligt aan onze “bekrompen” methodes om die zeer kleine massa-afname te kunnen constateren. c2 = 10 exp 17; reken maar eens uit hoe weinig massa het kost om bijvoorbeeld een kilojoule op te wekken!
Geachte heer Bijvoets,
Bedankt voor je reactie en je kritische evaluatie.
Je hebt gelijk dat die lucht onderin de waterkolom is samengedrukt en dat de luchtbel expandeert wanneer hij omhoog gaat. Een liter lucht aan het oppervlak – dat is 0.67 liter als het onder 5 meter zit. Die “delta h” in de tweede figuur verandert dus iets in de loop van het omhoog gaan van de luchtbel. Je kunt die expansie van die luchtbel uiteraard niet als bron van “vrije energie” gebruiken. Om die luchtbel van een liter in te brengen op 5 meter diepte zal je hem ook eerst moeten samenpersen van één tot 0.67 liter.
Onder de parallelle Nederlandstalige versie van het stukje is Jan Willem hiermee ook aan het rekenen gegaan.
Wanneer je het horizontaal oppervlak A van die kolom groter maakt, dan zal “delta h” inderdaad kleiner worden. Het product A maal “delta h” zal echter constant blijven en gelijk aan het volume van de ondergedompelde lucht. Het boven beschreven principe blijft opgaan. Stel je dompelt een pingpongballetje onder in het IJsselmeer. Het waterpeil in het IJsselmeer zal hierdoor misschien een nanometer of picometer omhoog aan. Maar het systeem kan uiteindelijk energie (potentiële energie van het IJsselmeerwater) verliezen door dat nietswegende balletje omhoog te duwen en het waterpeil van het gehele IJsselmeer die nano- of picometer te doen dalen. Het proces beschreven in het bovenstaande stukje met die tweede figuur, dat is waarom de Wet van Archimedes is zoals ze is.
Met dat energiebehoud zit het iets anders. Het is eigenlijk geen empirische wet. Het is NIET iets dat we al een miljoen maar gezien hebben en waarvan we dan maar veronderstellen dat het ook de miljoen & eerste keer weer zal opgaan. Energiebehoud volgt uit het feit dat een experiment herhaalbaar moet zijn. Gelijke begintoestanden leiden tot gelijke eindtoestanden. Dat noemen we een tijds-translatie-symmetrie. Emmy Noether bewees ongeveer 100 jaar geleden dat je elke symmetrie ook als behouden grootheid kunt formuleren. En zo krijg je dus dat energiebehoud. Energiebehoud is eigenlijk een consequentie van het feit dat we naar herhaalbare fenomenen kijken. Apparaten als auto’s, radio’s computers, maar ook de Rosch generator – zulke apparaten worden geacht steeds hetzelfde te doen als je in dezelfde situatie op hetzelfde knopje drukt. Energiebehoud is dus impliciet in de gedachtengang achter alle werktuigen. Vandaar dat die perpetuum mobile’s de LOGICA geweld aan doen. Een perpetuum mobile is zoiets als 2+2=5!
In de loop van de laatste paar eeuwen is men zich van meer verschijningsvormen van energie bewust geworden. Zo’n tweehonderd jaar geleden werd uitgevogeld dat warmte een vorm van energie is. Zo’n honderd jaar geleden bleek dat ook massa een vorm van energie is (en dat energie massa heeft). Wanneer je hout verbrand wordt chemische energie omgezet in warmte. Nadat de warmte is afgevoerd zullen de verbrandingsproducten dus een iets kleinere massa hebben dan het oorspronkelijke hout & zuurstof. Inderdaad bijna onmeetbaar klein omdat, zoals je aanstipte, c^2 zo groot is.
Dear Mr. or Mrs. Bijvoets, this is a comment under an English text, so I take the liberty to discuss in English.
I adress the claim that (according to you) an object submerged in an infinite sea would not lift a column of water by any amount, it would just displace the water sideways.
If this was true, one wouldn’t need any downward force to push a block of styrofoam under water, and ships would sink immediately. Unfortunately there don’t exist infinite seas that we could use to test this claim.
So I take just a big sea, with an area A on the surface. You may take A 100 square meters or a billion light years. It doesn’t matter. That’s the advantage of using letters. I bring a cube of styrofoam measuring 0,1 meter on each side to a certain depth into that sea. Let’s say that the bottom of the cube is at a depth of D meters.
We may agree that the water beneath D meters is not disturbed. So we are going to study what happens to
the potential energy of the totality of the water at depths less than D meters below the original sealevel.
The volume of all this water was AD cubic meters. After insertion of the styrofoam the water plus styrofoam occupies AD + 0.001 cubic meters. As the area is A the bottom part of the styrofoam block is now at
(AD + 0.001)/A below the surface of the water. This new depth equals D + 0.001/A meters.
So if we consider the difference between the two situations, then we have in the new situation one small cube of water missing with an average depth of D-0.05 meters, but a thin layer of water on top with a thickness of 0.001/A meters, and a total volume of 0.001 cubic meters. The mass of both the removed cube and the thin layer are both 1 kg, so there is conservation of mass (which would also problematic to check in in an infinite sea…). But taking sea level as zero level (we could also take the bottom of the sea as zero
level, the choice of zerolevel is arbirary) , the potential energy of the thin layer is
0.0005/A meter times g times 1 kg, and of the removed cube it was – (D-0.05) meter times g times 1 kg.
Now suppose A is very large. 0.0005/A we consider to be zero. In the second situation we see
the water is lifted over a distance of D-0.05 meters, gaining in potential energy (D-0.05) meter times g times 1 kg (if you check the dimensions, distance x acceleration x mass has the dimension of energy).
One could visualize this process as lifting a square column of height D and crosssection one square decimeter over a distance D, and after that spreading the top 10 cm that is lifted above sea level over the total area A of the sea into a thin layer.
If A is not very large, for instance barely larger than 0.01 square meter (i.e. the area of the top surface of the
cubic styrofoam block) then the term 0.0005/A meter times g times 1 kg is quite large. But that is also easy
to understand. If you push the styrofoam block under, the water level increases a lot, and already when you have pushed the block a few mm down the water level is already above the block. So you have to press with the full 10 newton (I take g=10 meter/sec^2) force. Ordinarily, with a large A the force needed to press the
styrofoam down gradually increases form 0 newton to 10 newton, and the value 10 newton is reached only when you have pressed the block down over (about) 10 cm.
If you are playing with situations were boats (for instance) in very small ponds are loaded with extra weights, then careful bookkeeping of the potential energy of the water may even be a convenient trick to
figure out what happens.
As I explained elsewhere, the hydrostatic pressure can also be interpreted this way.
We just take a piece of steel and insert it in the water at a certain depths. The water presses on all sides. What is the pressure? Look at one small piece of area, with area O of the object. It is pushed inside by the pressure, let’s say by d meters. (d may be a few nanometers…) so at that place we get a volume Od of water extra. A column of crosssection O and height h (the distance of O below the surface) shifts down over a distance d, so the net potential energy difference is volume x h x r (r is is the specific weight of the fluid). If we divide by d, then we find the force that has acted over the distance d, and if we divide by O we get the pressure. So hr is the hydrostatic pressure in this case.
Maybe the explanation of Bier suggested that the energy needed for bringing a block of styrofoam into water was used for raising the water level. Not so. It is used for effecting a net transport of water at a certain depth to the surface.
that has acted
Jan-Willem,
Good initiative to stick to English here. I just want to react to what you write in your very last paragraph.
Energy is necessary to take a piece of styrofoam and insert it at a depth H into a column of water as in the figure in the blog article. For convenience, imagine a disk shaped piece of styrofoam that has the same horizontal cross-sectional area A as the column of water in the drawing. Imagine that the thickness of this piece of styrofoam is dh. For the calculation of the amount of energy it actually does not matter whether you imagine (1) that the water column above the styrofoam is lifted by dh or (2) that a volume of water of dV = (A dh) is brought from a depth H to the surface.
Let “s” be the density (kilograms per cubic meter) of the water and consider the density of the styrofoam negligible compared to that of the water. Following (1), we realize that a column of water of length H has a mass M=sAH. Lifting it by dh requires and Energy E1=Mg dh = sAgH dh (g is the acceleration of gravity). Following (2), we take a volume of water equal to the volume of the styrofoam, i.e. dV = A dh. We take that volume’s mass m = s dV and we lift this mass up over a height H. This gives E2 = m g H = s A dh g H.
We see that indeed E1 = E2. Had it been different, by the way, we would have had the basis for a beautiful design of another perpetuum mobile: Take away some water from depth H, leave a hole there, bring the water to the surface and let the whole column drop to refill the hole. Run this process in a cycle and … Free Energy!!!
My picture of lifting the column is, of course, a little closer to what happens in reality. When you inject air at a depth H, you don’t teleport water against gravity from depth H to the surface. Instead, you do push up water that is above the air.
Let A be an initial state with energy E(A). Let B be a final state with energy E(B). In our case, state A is before we put the piece of styrofoam in the water and B is the state with the styrofoam disk at depth H. What we see above is a manifestation of the fact that, in a conservative (i.e. frictionless) field, the route from A to B does not matter. The energy difference E(B) – E(A) depends only on state A and state B.
Martin, of course we agree completely. My explanation was aimed at explaining to Bijvoets that in a very large ocean one still might see the process of insertion of a volume into water as having a *netto effect* of lifting water to the surface.
One might explain hydrostatic also in the way I learnt it in physics class when I was 15. Image a cubical block of water with imaginary walls in the water. This block is completely stationary. That means that the balance of forces on the block is zero. The water presses from above and below. The balance of these
pressur forces must equal the force of gravity on the block. From that you can see that the hydrostatic
pressure must equal depth times specific weight of the fluid.
Why is then is there also hydrostatic pressure on the sides of the block? This must be so, because when
push in a block sideways into the water at some depth, you also experience pressure. Moreover, if you press a water filled balloon from above and below you already will see the balloon expanding sidewards. This of course also doesn’t happen with the block with imaginary walls.
When there is pressure of whatever kind in a fluid, each surface experiences the same pressure. If this wasn’t so, one couldn’t have hydraulic installations. Basically the rerason is that the minute parts of the fluid can almost frictionless deform into any shape, and that in its turn is caused by the fact that fluid consist of molecules that can slide past each other. If there is pressure, it is because the molecules are all on average a bit closer to each other.
So when one pushes a styrofoam block horizontally into water it is still the case that the effect is that you lift a column of water vertically. (This explanation is strictly meant for people that don’t understand hydrostatic
pressure, i.e. who forgot what they learnt in school when they were 15 and who still don’t know what Archimedes had figured out over 2200 years ago, and of course also for those haven’t (yet) had
physics in school at all.)
Incidentally, the idea to explain basic physics by energy principles is an invention of 18th century scientists.
It is somewhat annoying to see people building perpetual motion machines of such simple design that scientists of 250 years ago already could have explained why it can’t work.
In Lowest position small tanks are half filled by air. Bubles in tanks will be bigger in higher position. If tower in about 10 m high bubles volume in highest position is about double and force too. Finally you can get 1,5 times more energy out than you used for half filling of the tank. But nergy for that is from bubles air – voume increases and therefore they cool down. Heat energy is from water of tower and to tower from enviroment. During running water temperature goes down. Short Power Output means that there is not any friction and compressor efficiency must be 100%, no turbulation, no increased enthrophy, etc.
My understanding is this: When rising through the water, the bubble volume expands liearly. This results in qudratic dependency between the depth and the total work performed by a rising bubble. Work required for creating a buble of a given volume is linearly proportional to the depth. This explains why there is positive energy extracted from the system, but this energy difference must come from outside the system…